近日，中国科学技术大学郭光灿院士团队何力新研究组取得突破：提出了广义Neumann定理，统一解释了传统铁电与新近发现的分数量子铁电（FQFE），修正了长期以来在铁电材料研究中的经典理论。这一成果为理解和调控铁电性质提供了全新思路。相关研究成果以“Generalized Neumann’s Principle as a Unified Framework for Fractional Quantum and Conventional Ferroelectricity”为题，9月9日发表在国际知名学术期刊《物理评论快报》上。

铁电作为一种基本的物理效应，不仅是凝聚态物理的重要研究方向，更是推动新一代信息技术与智能器件发展的关键，在非易失性存储器、智能传感、红外探测，以及未来量子信息技术等领域展现出广阔的应用前景，因此长期以来备受学术界与产业界的高度关注。

在铁电研究中，Neumann定理被视为判定铁电性的基本准则而写入教科书。然而，近年来科学家们在一些晶体中发现了一类全新的铁电现象：分数量子铁电（Fractional Quantum Ferroelectricity, FQFE），表现在某些高对称结构中，出现可翻转的分数量子的电极化，与经典Neumann定理的结论相矛盾。以单层In₂Se₃为例，其C_3v对称性按理不应产生面内极化，但计算与实验均证明其存在可翻转的面内极化，成为分数量子铁电性的典型案例。

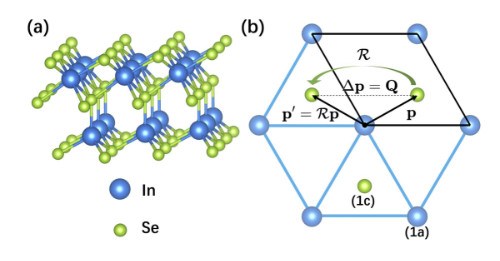
在本研究中，何力新教授与博士生庞鸿升提出了广义Neumann定理，首次建立了一个能够同时涵盖传统铁电与分数量子铁电的统一理论框架。传统的Neumann定理判断晶体是否允许出现铁电极化的数学形式为:Rp=p,其中R表示晶体的对称操作，p表示电极化。按照这一关系，只有当电极化在晶体所有对称操作下保持不变时，铁电性才可能存在。这一定理长期以来被视为“铁电性的基本原则”。在本研究中，研究人员提出了广义Neumann定理：Rp=p+Q，其中Q是整数量子的电极化。当Q=0时，这一定理退化为传统形式；而在更一般的情形下，它能够自然解释分数量子铁电性的存在。

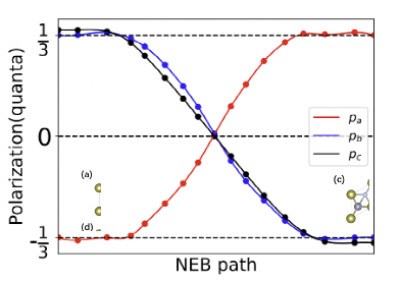
基于这一推广定理，研究人员系统分析了全部32个晶体点群，找到了所有可能存在的分数量子铁电形式，并通过高通量计算，发现有大量此前被认为不可能出现铁电行为的材料，其实都允许铁电极化的存在。更重要的是，其中许多材料的极化不仅存在，而且能够翻转，具有潜在的实际应用价值。文章以HfZnN₂材料为例，研究了其面内分数量子极化可通过与面外极化耦合实现翻转的路径和势垒。

广义Neumann定理为传统铁电与分数量子铁电建立了统一的理论框架，不仅为分数量子铁电的起源提供了简洁清晰的物理图像，也奠定了坚实的理论基础，被认为有望改写铁电研究的教科书。分数量子铁电性为铁电家族开启了新的篇章，由此发现了大量此前未被认识的铁电材料，进一步拓展了铁电效应的内涵。由于目前对这些材料的研究仍然有限，它们很可能展现出许多传统铁电材料所不具备的独特性质，因此具有广阔的探索前景和重要的应用潜力。

博士生庞鸿升为本文第一作者，何力新教授为通讯作者。该研究受到了中国科学院，国家自然科学基金委等的支持。