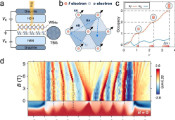
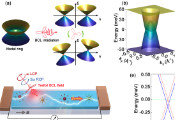
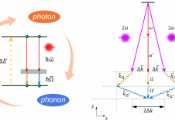
无限分量BF场论:分形子序、托普利茨编织与非厄米放大的交汇点
基于李等人近期关于托普利茨编织的研究[《物理评论B》110卷205108期(2024年)],该研究团队通过沿第四空间维度(w方向)堆叠拓扑BF理论并以平移不变方式耦合,提出了无限分量BF理论(iBF)。该框架可描述四维分形拓扑序的低能物理行为,其中粒子和环状激发均在堆叠方向上呈现受限迁移特性,其粒子-环形编织统计由非对称整数值托普利茨K矩阵编码。研究人员发现了一种新型粒子-环形编织形式——源于K矩阵边界零奇异模式(ZSM)的托普利茨编织。在热力学极限下,即使粒子与环形激发位于相反的三维边界,非平凡编织相位依然存在,因边界ZSM主导着K⁻¹矩阵非零非对角元并调控边界驱动的编织行为。通过对具有羽达野-尼尔森型及非厄米Su-Schrieffer-Heeger型托普利茨K矩阵的iBF理论进行解析与数值研究,证实了ZSM与托普利茨编织的对应关系。该理论构建架起了强关联拓扑场论与非相互作用非厄米物理间的桥梁,其中ZSM正是非厄米放大效应的物理基础。潜在扩展方向包括:由扭曲拓扑项诱导的三环形及博罗梅安环托普利茨编织、广义纠缠重整化、以及iBF理论中的叶状结构。文中还简要讨论了与平行宇宙场景的启发性类比。