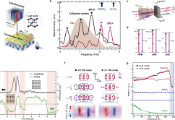
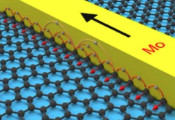
手性带隙态普遍为非拓扑态
该团队提出了一种关于2+1维手征有隙基态中圆形区域纠缠哈密顿量的Li-Haldane猜想的算子扩展。该逻辑适用于具有尖锐拐角的区域,据此该团队推导出了关于拐角纠缠的若干普适性质。这些普适性质源于对波函数的一组局部可检验条件。此外,该团队还定义了一个反映拐角纠缠贡献稳健性的量(ctot)min,并证明其为有隙边界的存在设置了障碍。该研究的一个显著成果是:该团队可以从给定波函数出发,在同一手征有隙相中构建局域有隙哈密顿量;该团队推测该哈密顿量比原始母哈密顿量更接近低能重整化群不动点。对拐角纠缠的分析揭示了手征有隙态体区纠缠结构中隐含的普适共形几何的涌现现象,而这一现象在拓扑场论中不可见。
量科快讯
2 分钟前
【牛津大学开设量子技术理学硕士课程 首批有29名学生入学】英国牛津大学新开设的量子技术理学硕士课程已于近日正式启动。首批有29名学生入学,他们将率先受益于这一面向快速发展的量子技术领域的跨学科培训课…
23 小时前
1 天前
2 天前
2 天前
2 天前