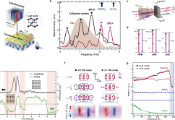
验证与学习量子伊辛哈密顿量
该工作中,研究人员致力于量子伊辛哈密顿量的验证与学习问题,主要贡献如下:
伊辛哈密顿量验证:研究证明通过其时间演化算子以归一化Frobenius范数验证伊辛哈密顿量仅需O~(1/ε)次时间演化,该结果与Ω(1/ε)的海森堡标度下界仅相差对数因子。据团队所知,这是首个实现近乎最优的哈密顿量性质测试算法。分析过程中采用傅里叶分析中的博纳米引理成为关键要素。
伊辛吉布斯态学习:该团队设计了一种在迹范数下学习伊辛吉布斯态的算法,其样本效率在所有参数维度均表现优异。相较而言,此前方法虽然能通过学习底层哈密顿量(隐含吉布斯态学习)实现目标,但存在逆温度参数维度样本复杂度指数级增长的缺陷。
伊辛吉布斯态验证:针对安舒(《哈佛数据科学评论》2022年)提出的问题,该工作给出一种在迹范数下验证伊辛吉布斯态的算法,同时具备样本高效性与时间高效性。
最终,研究人员将吉布斯态学习与验证的成果拓展至任意常数k值的广义k-局域哈密顿量体系。