费米高斯态的可扩展性
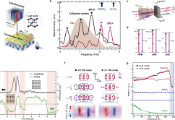
该研究团队对费米子高斯态的(k₁,k₂)-可扩展性进行了研究,这一性质在量子关联和可分离态近似中具有核心作用。研究表明,这些态具有(k₁,k₂)-可扩展性当且仅当它们允许费米子高斯扩展,从而获得完整的协方差矩阵表征,并构建了一个规模与模式数量呈线性关系的半定规划(SDP)程序。该方法为任意费米子态提供了必要条件,且在高斯体系下具有充分性。
主要成果体现为有限de Finetti型定理:研究人员推导出(k₁,k₂)-可扩展费米子高斯态与可分离态之间的迹范数边界,将先前指数级缩放改进为模式数量的线性关系,并补充了相对熵与压缩纠缠边界。对于双模系统,上下边界在1/√(k₁k₂)量级完全匹配。可扩展性还为费米子系统中的可分离性概念提供了操作支持。
最后针对费米子高斯信道,该工作提出了反降解性的SDP判定准则,并证明纠缠破坏信道等价于置换信道,这意味着不存在非平凡的纠缠破坏型费米子高斯信道。