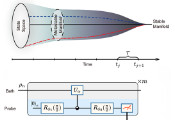
基于马尔可夫嵌入连续监测非马尔科夫量子体系的物理降维随机方程
模拟非马尔可夫量子系统的一种有效方法是将目标(量子)系统嵌入到一个更大的量子系统中。常用的嵌入方式是引入一个被称为辅助系统的额外量子系统,该辅助系统与主系统耦合,且二者均可耦合至量子白噪声过程。主系统与辅助系统共同构成一个量子马尔可夫系统,而量子白噪声则充当该系统的浴(环境)。最新研究表明,在这种嵌入框架下,通过行波量子探针连续监测时,主系统的条件演化可表示为仅包含主系统算符的耦合随机微分方程组(SDEs)。仅由测量结果决定的约化条件态完全由该耦合SDE方程组的"对角块"确定。本文证明:在初始条件允许的情况下,"非对角块"可被精确消除,从而得到仅包含对角块的简化封闭SDE方程组。在附加条件下,非对角初始条件甚至可以完全消弭。这个新的封闭方程组包含涉及双时间随机核的积分项,表征了连续测量下主系统的非马尔可夫随机动力学。该方程组决定了主系统的约化条件态,可视为连续监测非马尔可夫量子系统的随机中岛-兹万齐格型方程。
量科快讯
【中国移动申请的一项量子比特映射方法发明专利进入公示阶段】国家知识产权局最近公示的信息显示,中移(苏州)软件技术有限公司与中国移动通信集团有限公司联合申请了一项名为“量子比特映射方法、装置、设备、介…
14 小时前
15 小时前
19 小时前
19 小时前
20 小时前
【安恒信息申请一项基于量子密钥的数据安全传输技术发明专利】据国家知识产权局最近公示信息,杭州安恒信息技术股份有限公司申请了一项名为“基于量子密钥的数据安全传输方法、装置、设备及介质”的发明专利(申请…
1 天前
【中国移动申请一种基于量子迁移的遥感图像识别方法发明专利】据国家知识产权局近日公示的信息,中移(苏州)软件技术有限公司与中国移动通信集团有限公司联合申请的发明专利“基于量子迁移的遥感图像识别方法、系…
1 天前
【AQT的囚禁离子量子计算机现已在亚马逊Braket上架】欧洲领先的量子计算机提供商AQT日前宣布,其离子阱量子计算机IBEX Q1现已通过亚马逊云服务(AWS)上线,从而为全球用户提供了云端访问欧…
1 天前
1 天前