利用张量网络提升二项式奇异期权定价
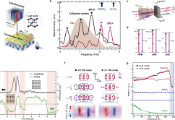
奇异金融衍生品(如亚式期权与多资产美式篮式期权)的定价对传统数值方法(如二叉树法或蒙特卡洛法)构成显著挑战。前者常随目标参数呈指数级复杂度增长,后者则需昂贵模拟才能实现统计收敛。该研究将期权定价的二叉树法与张量网络技术(特别是矩阵乘积态MPS)相结合以攻克这些难题。所提方法相较传统手段能以线性复杂度处理目标参数,显著降低奇异期权定价的计算负担。针对亚式期权,该团队提出两种方法:基于张量列车交叉逼近的定价算法,以及提供严格价格下界的MPS变分定价法;针对多资产美式篮式期权,研究人员将解耦树技术与张量列车交叉逼近结合,可高效处理多达8种关联资产的组合。所有方法在亚式期权的离散化步骤数N、多资产期权的资产数m维度上均保持线性复杂度。数值实验证实,张量网络方法作为金融工程的高效模拟与优化工具具有巨大潜力。