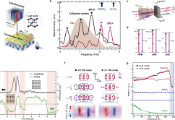
周期性驱动哈密顿量的Floquet信息学习
表征时间周期性哈密顿量对于验证和控制驱动量子平台至关重要,然而当前未经调整的重构方法需要密集的时域采样和繁重的后处理。该研究团队提出了一种可扩展的基于Floquet理论的学习算法,将哈密顿量表示为截断的傅里叶级数,并在Floquet能带图中将参数估计重构为紧凑的线性逆问题。该算法非常适合满足温和平滑性/带宽限制条件的问题。在此机制下,其采样复杂度和运行时复杂度随傅里叶截断数、时间分辨率及未知系数数量呈多项式增长。对于局域哈密顿模型,系数随系统规模呈多项式增长,导致对希尔伯特空间维度的依赖至多为多对数关系。此外,在一维和二维伊辛模型与海森堡晶格上的数值实验显示出算法对时间分辨率的快速收敛性以及对高阶微扰的鲁棒性。自适应规则可学习傅里叶级数的截断点,无需事先设置已知截断条件。这些特性使得该算法能有效认证和基准测试具有快速衰减高阶项的周期性驱动平台,并可自然扩展到近周期性驱动场景。