量子科技中心_量科网

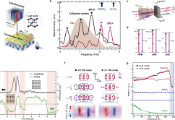
该研究团队研究了SU(N)自旋系统，这些系统模拟了N=2和3维德西特空间中粒子的行为。其哈密顿量描述了一个具有双曲不动点的动态系统，在量子层面会产生涌现的准正态模式，这些模式表现为态密度中的准粒子峰。针对二维德西特空间中的粒子，研究人员从具有经典相空间两个双曲不动点的PT对称Lipkin-Meshkov-Glick模型中，发现了主系列和补充系列的态密度。随后该工作系统研究了这类模型的不同光谱和动力学特性，包括能级间距统计、两点函数、平方对易子、光谱形状因子、Krylov算符及态复杂度。研究发现，虽然这些特性的早期行为受鞍点支配（在某些情况下会表现出类似混沌系统的特征），但对其晚期行为的深入观察揭示了该体系的可积本质。