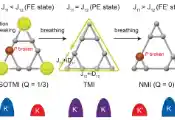
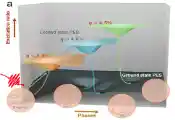
南京大学张谷课题组揭示阿贝尔任意子编织新过程和编织关联的量子纠缠
近日,南京大学物理学院张谷副教授课题组与法国巴黎萨克雷大学、德国卡尔斯鲁厄理工学院、以色列魏茨曼研究院等机构研究团队展开合作,在任意子物理与量子纠缠交叉领域的研究中取得重要进展,提出并实验验证了一种全新的阿贝尔任意子(abelian anyon)编织过程,并且量化与该过程关联的量子纠缠。研究团队通过一种“类安德烈夫隧穿”(Andreev-like tunneling)过程[见图1, 2],巧妙地理论提出并且实现了一种全新的“任意子-准空穴编织”(anyon- quasihole braiding)过程,并进一步在两个独立的任意子系统间建立了由其分数统计特性诱导产生的量子纠缠。该工作不仅揭示与验证了分数统计与量子纠缠的深刻内在联系,还开发出一种基于电流噪声,可实验测量的“纠缠指针” (entanglement pointer)来对纠缠进行量化,为探索和操控任意子提供了新思路。相关研究成果以“Fractional-statistics-induced entanglement from Andreev-like tunneling” 为题 发表 于Nature Communications [Nat. Commun. 16, 6558 (2025)]。
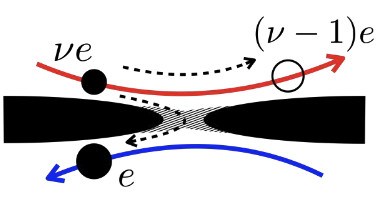
任意子的奇异编织特性是拓扑量子技术的基石。理论上,通过“编织” (braiding)任意子的世界线,可以构建天然抵抗局域噪声的量子比特,这是实现容错拓扑量子计算的核心优势。然而,尽管近年来在探测任意子,尤其是其编织特性方面取得了令人鼓舞的进展,但一个关键问题仍悬而未决:我们是否,以及如何能够利用任意子的编织来产生可被验证的量子纠缠?针对这一问题,研究人员在一个由填充系数𝜈 =1/3的分数量子霍尔效应(fractional quantum Hall) 边缘态构成的平台中进行了理论与实验探索。在该平台中,两个携带任意子的通道由一个仅允许电子(费米子)隧穿的量子点接触相连[见图1]。由于任意子与电子的编织相位是平庸的,传统观点认为此装置无法产生与任意子编织统计特性相关联的纠缠和输运现象。
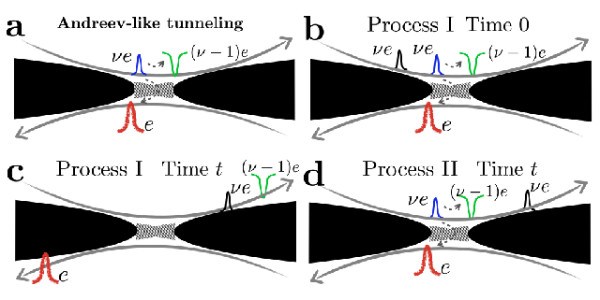
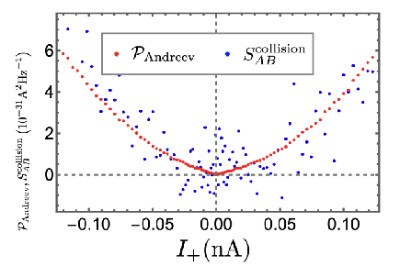
然而,课题组在该装置中发现了一种全新的任意子编织过程[见图2]。具体而言,在Laughlin系统中,当一个电子隧穿时,会在其原始通道中留下一个“准空穴”(quasi-hole)。随后,通道中流动的任意子会与这个由隧穿事件激发的准空穴发生有效的编织。这一全新任意子编织过程被研究团队命名为“任意子- 准空穴编织”。这种全新编织过程导致两个任意子通道之间的量子纠缠明确地依赖于任意子的分数统计编织相位。为了量化这种新发现的纠缠,团队将一个先前用于费米子和玻色子的理论工具——“纠缠指针”——推广到了任意子体系。 该指针是一个基于系统跨通道电流噪声的函数,它能够捕捉并量化由任意子分数统计所贡献的纠缠部分。理论预言与实验数据高度符合[见图3]。
该工作首次揭示了类安德烈夫隧穿极限下的编织现象,并且在理论和实验上系统地揭示了由任意子分数统计诱导产生的量子纠缠,深化了我们对拓扑物态中量子信息现象的理解。更重要的是,这一理论框架为未来研究开辟了广阔前景。 研究人员指出,该方法可能被推广至更奇特的准粒子体系,特别是作为拓扑量子计算基石的非阿贝尔任意子。通过测量由非阿贝尔统计诱导的纠缠,科学家们将能够更精确地区分候选的拓扑物态,并最终实现对拓扑量子比特的操控。这项工作不仅深化了我们对基础物理现象的理解,也为探索基于拓扑物态的新型量子技术提供了新的思路,在凝聚态物理、量子信息和量子计算等领域展现出重要的应用前景。
南京大学物理学院为该工作第一完成单位,南京大学物理学院张谷副教授为第一作者,法国巴黎萨克雷大学Frederic Pierre教授,德国卡尔斯鲁厄理工学院Igor Gornyi教授,以及以色列魏茨曼研究院Yuval Gefen教授为通讯作者。 共同作者还包括瑞典隆德大学Pierre Glidic博士。该工作得到南京大学启动基金,国家自然科学基金面上项目,科技创新2030重大研究计划,以及人工微结构科学与技术协同创新中心与江苏省物理科学研究中心的支持。