近日，复旦大学物理学系周洋课题组提出了处于混合态下的量子系统的多体关联度量——“反射多体熵（Reflected Multientropy）”，并运用理论计算的手段验证了其全息对偶。该项研究成果于近期在线发表于Physical Review Letters，论文链接：https://journals.aps.org/prl/abstract/10.1103/76vs-rxcs

量子纠缠是理解AdS/CFT对偶（又称全息对偶）和量子引力本质的核心工具。著名的Ryu-Takayanagi公式建立了边界场论的纠缠熵和体时空几何之间的联系，发现这一联系的两位科学家Ryu和Takayanagi因此获颁2024年狄拉克奖章。然而，纠缠熵仅能度量纯态系统的两体纠缠，实际物理系统常常处于混合态，纠缠结构也不局限于两体。将传统纠缠熵拓展为多体的、混态的关联度量并寻找其全息对偶，可以帮助理解时空几何如何从边界量子系统的多体纠缠中涌现出来。

为了解决这一难题，复旦大学物理学系周洋课题组创新性地将正则纯化（Canonical Purification）与多体熵（Multientropy）的思想相结合，提出了一种适用于混态体系的多体关联度量——反射多体熵（Reflected Multientropy）。这一新量度既继承了多体熵在刻画多体量子纠缠方面的优势，又通过纯化构造有效规避了纠缠熵及多体熵在连续量子场论中普遍存在的紫外发散问题，从而成为一种在场论层面内禀定义良好的多体关联度量。这一度量为理解多体纠缠与时空几何的对应关系提供了新的工具。

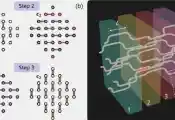
在此基础上，研究小组进一步提出了反射多体熵的全息对偶：边界场论中的反射多体熵对应于引力理论中“极小曲面网络”（Minimal Surface Web）的面积。为了验证这一猜想，研究小组在低维数的AdS/CFT框架下完成了严格的检验——在边界场论中计算扭转算子的六点关联函数，并将其与对偶几何结果进行比较，发现两者在零温与有限温度情形下均精确吻合。这一高度吻合不仅为反射多体熵的全息对偶提供了有力证据，也展示了其在研究混态多体关联以及量子引力中的潜在应用价值。

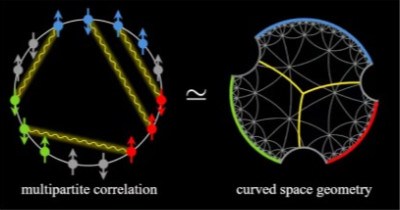
本研究不仅开辟了混态多体纠缠全息对偶的新方向，更为理解“时空几何源于量子纠缠”的深层物理机制提供了线索。

该工作由复旦大学物理学系周洋课题组独立完成。论文的通讯作者为周洋，其他两名作者为课题组博士生袁马轲和李明懿。研究工作获得国家自然科学基金（项目号：12375063）、上海市自然科学基金（21ZR1409800）以及上海人才发展资金资助。