近日，南京大学物理学院陈伟教授课题组在非厄米对称性破缺机制的研究中取得进展，提出了一种普适的量子-经典对应原理（quantum-classical correspondence），在每一个能级的实数或复数性与其对应的半经典轨道对称性之间建立了精确对应。该工作揭示了非厄米对称性破缺的一般性物理机制，为非厄米能谱提供了完整的理解，其物理视角对非厄米效应的精确调控及其相关应用具有重要意义。

在量子力学中，厄米哈密顿量对应实数能谱；而当系统的有效哈密顿量为非厄米时，其能谱性质变得更加丰富，这是非厄米物理研究的核心问题之一。对于具有赝厄米对称性（Pseudo-Hermitian symmetry）的一大类非厄米哈密顿量而言，其能级要么是实数，要么形成复共轭对。以宇称-时间（PT）对称系统为例，系统参数的改变会引发实数能谱向复数能谱的转变，称为PT相变，并伴随相应本征态的自发对称性破缺。然而，与传统相变理论中受最小自由能原理支配的自发对称性破缺不同，非厄米对称性破缺随模型参数变化自然发生，目前尚缺乏普适物理机制。在一项开创性研究中，Bender和Boettcher基于特定模型，从半经典角度对其中发生的PT转变提供了物理解释。但该理论仅适用于特定模型以及PT对称，并且该工作以及相关后续研究都只关注能谱的整体性质，并未对其提供完整的理解。这引出了一个重要问题：在非厄米物理中，是否存在一种能够精确刻画每个能级性质及其对称性破缺的普适物理机制，并且可以广泛适用于具有不同赝厄米对称性的物理系统。

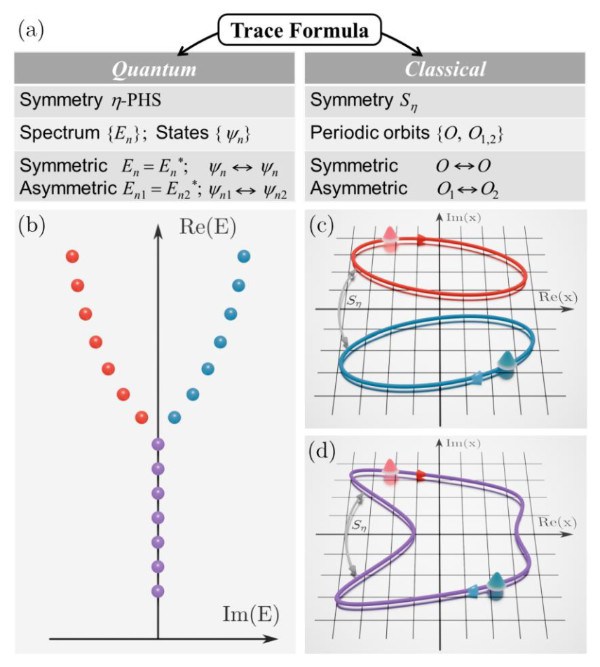
 针对这一科学问题，课题组基于复数路径积分方法发展了广义 Gutzwiller 求迹公式，从而在单个能级的层面建立起其实数-复数特性与对应半经典轨道对称性之间的量子-经典对应关系（参见图1）。具体而言，作者首先指出，任何满足广义η-赝厄米对称性 ηH(x,p)η-1=H†(x,p)的系统，其对应的经典哈密顿量将具有一种称为Sη的半经典对称性，即 H(xη,pη)=H*(x*,p*)。数学上可以证明：当某一半经典轨道O具有Sη对称性时，沿着该轨道进行量子化将产生实数能级En；反之，当存在一对轨道O1和O2，它们各自破坏Sη对称性但彼此构成一个Sη对，那么分别沿这两条轨道进行量子化将产生成对出现的复共轭能级En1 = En2*（参见图1）。

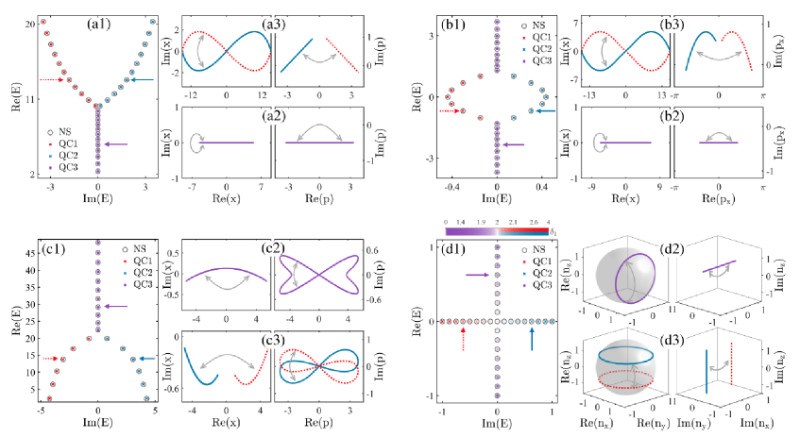
为了验证该理论的正确性，作者选取了三种具有不同赝厄米对称性的连续模型进行检验，分别是时间反演（T）对称性，镜像-时间反演（MT）对称性以及PT对称性。计算结果验证了广义 Gutzwiller 求迹公式及其对应量子化条件在求解非厄米能谱方面的正确性，并进一步证明了量子-经典对应关系在单个能级层面的适用性（参见图2(a–c)）。此外，该工作进一步采用复数自旋路径积分方法，研究了具有PT对称性的非厄米二能级系统，并证明量子-经典对应关系在离散模型中同样成立（参见图 2(d)）。更进一步，该工作还在复数路径积分框架下对非厄米奇异点（exceptional point）获得了全新的物理理解，揭示了其本质上是一种纯量子效应，因其无法通过单一经典轨道加以描述。具体而言，对于连续模型，在奇异点附近，轨道之间的隧穿效应变得至关重要；而在二能级系统中，奇异点对应的经典轨道出现发散行为。

该工作不仅深化了我们对非厄米物理现象的理解，更为其精确调控提供了崭新的视角。该理论框架适用于一般性的非厄米物理问题，可广泛应用于量子物理、凝聚态物理、光学与声学等多个领域。

相关研究成果以“Quantum-Classical Correspondence of Non-Hermitian Symmetry Breaking” 为题发表于Physical Review Letters [Phys. Rev. Lett. 134, 240201 (2025)]。南京大学物理学院为该工作第一完成单位，课题组博士生蔡卓廷为第一作者，博士生李海栋为第二作者，陈伟教授为通讯作者。该工作得到国家自然科学基金优秀青年科学基金、国家重点研发计划、江苏省自然科学基金、中央高校基本科研业务费、人工微结构科学与技术协同创新中心与江苏省物理科学研究中心的支持，在此表示感谢。