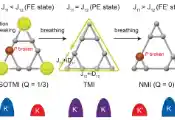
周期驱动下的奇异量子物态:超临界Floquet非费米液体
在凝聚态物理学中,“费米面”是一个核心概念,它描述了金属中电子能量的边界,深刻影响着材料的电性、磁性等诸多基本性质。通常,物理学家在热力学平衡的框架下研究物态。然而,一个有趣的问题是:当电子系统被周期驱动(即Floquet驱动,例如激光)而脱离平衡态时,费米面会发生什么变化?它是否依然存在?
一般认为,持续的驱动最终会导致系统被加热至无限高温度的平庸状态,从而抹去所有精细的量子特征,包括费米面。然而,近期的理论研究表明,情况并非总是如此简单。该研究揭示,当周期驱动的电子系统与玻色环境(例如晶格振动或声子)耦合时,系统可以演化到一个奇特的非平衡稳态——“Floquet非费米液体”。
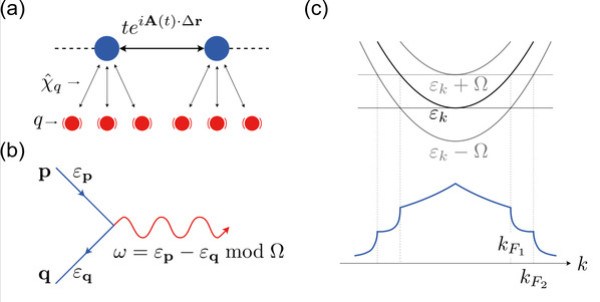
这项研究的核心发现是,在这个非平衡稳态中,电子的动量分布函数中会涌现出新的“Floquet费米面”。与平衡态下费米液体中截然分明(零温时)的跳变不同,这些Floquet费米面呈现出类似“非费米液体”的特征,表现为动量分布函数中的“扭折”(kink)或其他形式的非解析行为。
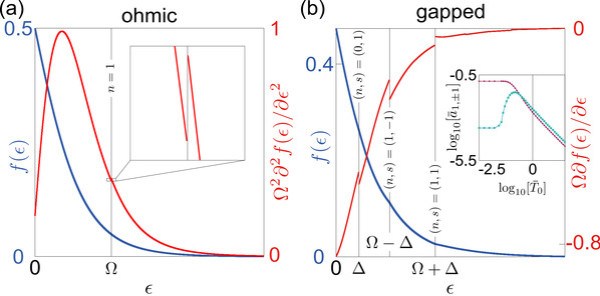
更令人惊讶的是,这些由非平衡效应导致的Floquet费米面,即使在有限温度下也能保持其尖锐的非解析特征,这种行为被称为“超临界”(ultra-critical)行为。这与已知的平衡态物理形成了鲜明对比:在平衡态下,有限温度会不可避免地“模糊”费米面,导致量子关联(如Friedel振荡)随距离指数衰减。然而,在这种Floquet非费米液体中,即使在有限温度下,量子关联仍然呈现幂律衰减,并且粒子-空穴激发谱的边界也保持尖锐。这表明周期性驱动不仅没有将系统完全“加热”,反而稳定了一种新奇的、超越热力学平衡的量子物态。
这项工作不仅挑战了我们对非平衡量子系统和有限温度物理的传统理解,也突显了环境(热库)在决定非平衡稳态性质中的关键作用。值得注意的是,如果将系统耦合到费米子热库而非玻色子热库,系统则会演化到另一种截然不同的稳态——“Floquet费米液体”,其动量分布函数呈现出具有多个跳变的“费米-狄拉克阶梯”形状。这一对比鲜明地揭示了驱动系统与不同类型环境相互作用时所产生的丰富物理现象。这项研究揭示了周期性驱动作为一种强大的调控手段,有潜力创造出在平衡态下无法实现的奇异量子物态,为探索和设计新奇量子材料与现象开辟了新的方向。
相关的研究成果以“Ultracritical Floquet Non-Fermi Liquid”为题,发表在国际物理学顶级期刊《Physical Review Letters》上。该工作由即将入职浙江大学量子物态与器件研究中心(CQM)的施李坤博士、新加坡南洋理工大学的Oles Matsyshyn博士和Justin C. W. Song教授,以及德国莱比锡大学的Inti Sodemann Villadiego教授合作完成。