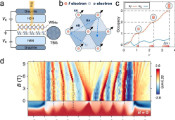
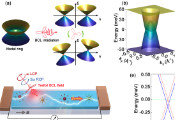
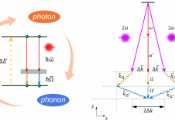
利用随机轨迹模拟多体量子动力学:对塔维斯-卡明斯模型的关键性测试
该研究团队批判性地探究了一种最新提出的采样框架在光相互作用多体量子系统动力学中的适用性,通过随机轨迹方法将其应用于封闭与开放型Tavis-Cummings模型(TCM)。这些随机微分方程(SDEs)通过模拟与量子算子关联的复值动力学变量,对正P相空间表示进行采样。随机轨迹的统计平均可得出量子力学期望值的演化过程。然而,针对TCM模型的数值实现表明该SDEs存在发散解——这种特性在其他相空间方法中也有记载。这使得该框架仅适用于有限的传播时间,且该时间窗口高度依赖系统物理参数与初始条件。研究人员阐述了这些发散现象的数学本质,并证明其对统计平均的关键贡献。为尝试正则化发散,该工作将SDEs转化为具有不同噪声实现的等效方程集,从而延展了有效时间边界。但随机轨迹方法无法再现TCM模型的量子塌缩与复苏现象,这揭示了随机相空间采样方法在具有显著量子特征系统中普遍存在的适用性困境。