量子科技中心_量科网

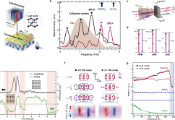
近日，一种基于张量化回流修正的变分波函数在求解费米-哈伯德类模型时实现了最先进的能量精度。然而该模型求解极具挑战性，方法的有效性需通过基态物理性质验证。本研究将这种张量化回流修正简称为“张量回流法”。研究团队将该方法应用于二维晶格（最大达256个位点）的费米-哈伯德模型，考察了不同相互作用强度U、电子填充数n及边界条件的影响。通过引入更多回流项（如次近邻或全位点回流修正），能量精度可进一步提升。在64位点晶格上的能量外推结果与键维度高达D=20的梯度优化fPEPS方法相当。对于开边界条件下16×16晶格n=0.875且U=8的情形，仅考虑近邻回流项所得能量就比当前最先进的D=20 fPEPS方法仅高4.5×10^-4。在周期性边界条件下，变分波函数未预设任何对称性约束，但仍成功观测到线性条纹序。当填充数相同且U=10、12时，基于U=8波函数初始化获得的能量低于直接优化结果，且与前沿张量网络方法相当甚至更优。对于n=0.8和0.9375的案例，直接优化结果与AFQMC获得的相图完全吻合。