量子科技中心_量科网

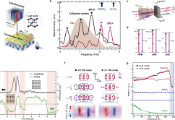
受击伊辛模型作为量子混沌模型已被广泛研究。Bertini、Kos和Prosen在热力学极限下研究了该系统，通过周期边界条件在自对偶点处给出了谱形因子K(t)的解析表达式。谱形因子是时间演化算子迹的二次矩，该研究团队在受击伊辛模型中进一步研究了这一随机变量的高阶矩。Flack、Bertini和Prosen先前对这些高阶矩的研究表明：当系统在自对偶点采用周期边界条件时，迹线会反常地表现为实高斯随机变量。与之形成鲜明对比的是，该工作研究了自对偶点处开放边界条件下的模型，发现时间演化算子迹线正如基于圆正交系综的随机矩阵普适性所预期的那样，表现为复高斯随机变量。这一结果凸显了边界条件对迹线统计特性的惊人强效影响。研究人员还研究了被称为洛施密特谱形因子的谱形因子推广形式，并给出了不同边界条件下的结果。