量子态的严格最大似然估计
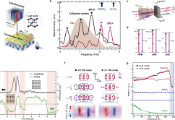
现有量子态层析方法由于计算和内存需求过高,其可扩展性受到限制,难以用于大规模量子态的恢复。该工作通过采用Burer-Monteiro分解重构最大似然估计(MLE)问题,实现了密度矩阵的非凸但低秩的参数化,从而突破这些限制。研究人员通过解析消除单位迹和半正定约束,推导出完全无约束的优化模型,从而避免了优化过程中的投影步骤。此外,该团队还预先确定了与单位迹约束相关的拉格朗日乘子,降低了计算开销。所得模型适用于可扩展的一阶优化方法,并通过有限内存BFGS(L-BFGS)算法验证了其可操作性。值得注意的是,该工作还提出了一种低内存版本的算法,能够基于泡利POVM测量完全恢复特定的大规模量子态。该低内存算法无需显式构建任何密度矩阵,也不要求密度矩阵具有矩阵乘积态(MPS)或其他张量结构。在固定测量次数和固定秩的条件下,该算法恢复d×d密度矩阵的单次迭代复杂度仅为𝒪(d log d)。此外,研究人员推导出了一个实用的误差边界,可用于建立严格的终止准则。数值实验表明,该方法在中等规模问题上与最先进算法性能相当,并成功在笔记本电脑上5小时内完成了20量子位问题的求解。