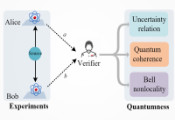
纠缠量子资源的三元组乘法
多方计算 (MPC) 的一个高效范例是围绕访问共享预处理计算资源构建的协议。在该模型中,某些形式的相关随机性会在参与者计算之前分发给他们。共享随机性随后会在计算阶段被消耗,该阶段涉及具有高效轮复杂度的公共通信。只要初始相关性被安全地分发,则计算在第二阶段是安全的。通常后者需要一些强设置假设,例如可信经销商和私有通道。该团队提出了一种从纠缠量子图态生成这些相关性的新方法,并在有限的假设条件下,提供了抵御恶意对手的信息论隐私保证。团队的主要贡献是一个基于三方资源状态和测量的协议,用于提取二进制乘法三元组,这是一种特殊形式的共享随机性,可以实现位连接的私有乘法。在这里,研究人员聘请第三方作为裁判,并要求三方中只有一对诚实的参与者。裁判员的角色比发牌员的角色弱,因为裁判员对传播的底层共享随机性一无所知。该团队证明了协议具有完美的隐私性,假设能够访问理想的资源状态副本,这一假设基于图状态验证协议的存在。最后,研究人员演示了它作为更复杂布尔函数的原语的应用,例如二选一无知传输 (OT) 和任意 N 方布尔函数的多方预测控制 (MPC),假设能够访问正确的广播信道。