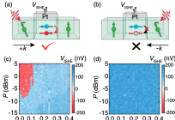
子系统复杂性的急剧转变
在时间演化的纯量子态中,电路复杂度随时间呈线性增长的现象可维持指数级时长。该行为已在特定模型中得到证明,并被推测适用于一般量子多体系统,同时被认为与AdS/CFT理论中黑洞内部长期增长的动力学存在对偶关系。如何建立混合态下类似的理论框架仍是一个重要问题。该研究团队聚焦纯量子态时间演化子系统的电路复杂度,发现当子系统尺度超过全系统一半时,其复杂度会与全局态类似地呈现指数时长范围内的线性增长;反之当子系统小于半系统时,复杂度会经历先升后降的过程,最终随子系统平衡回归低复杂度态。值得注意的是,这两种行为会在半系统尺度处发生急剧转变。研究人员运用全息对偶原理描绘了子系统复杂度的动力学图景,并严格证明了随机量子电路中这种突跃转变的存在。进一步地,通过全息理论预测了有限温度下复杂度增长的特征——这些特征是随机量子电路技术手段无法捕捉的。特别指出,在有限温度条件下,当子系统尺度小于临界值(该临界值本身小于半系统尺度)时,子系统复杂度会近乎瞬时饱和,而非呈现先升后降。这种新现象以及与半系统尺度以上转变的对应关系,为未来基于严格方法的研究提供了方向标。
量科快讯
2 天前
3 天前