量子科技中心_量科网

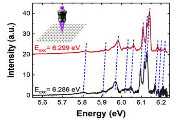
该研究团队对玩家可以使用量子策略进行互动的游戏的精确和近似最优性进行了表征。与作者之前的工作（arXiv: 2311.12887）相比，该工作应用了Ostrev于2016年提出的框架，用于构建超越CHSH和XOR游戏的误差界限，同时结合了确定原始可行解的良好半定规划的存在性以及量子-经典对偶间隙。进一步开发误差界限及其相关对象在多参与者博弈论场景中的构建仍然具有重要意义。在这种场景中，研究人员不仅会遇到每个玩家可能策略的显著更大的组合空间，还会遇到多个显著的量子优势机会。该工作通过描述XOR∗、编译XOR∗以及XOR∗游戏的强并行重复变体中的其他可能策略的变体，作为量子优势的潜在来源，总结了这一研究。